I-Ondes
acoustiques dans un tuyau sonore.[1]
Le but de cette partie est d’analyser simplement le principe d’émission sonore par une flûte et de comprendre les mécanismes permettant d’émettre une note juste à l’aide de cet instrument.
I-0. Résumé de ce paragraphe.
Pour expliquer l’émission de notes à l’aide d’une flûte et la façon de choisir la hauteur du son joué on doit expliquer ce qu’est un son, comment il est émis, quelles sont ses caractéristiques et comment le contrôler. Pour cela il faut rappeler qu’un son est produit par une mise en vibration de l’air. Les tympans sont mis en mouvement par une différence de pression entre l’air extérieur et l’oreille interne, ce mouvement étant interprété par le cerveau comme un son. On doit donc déterminer comment mettre en mouvement l’air et comment ce mouvement imprimé en un endroit se déplace pour atteindre l’auditeur. La mise en mouvement d’un objet initialement au repos est provoquée par des forces exercées sur l’objet (principe fondamental de la dynamique). C’est le cas pour l’air, il est mis en mouvement par une force. La force utilisée pour mettre l’air en mouvement dans une flûte est exercée par des muscles qui compriment les poumons. Cette compression va provoquer une augmentation de pression de l’air présent dans les poumons, cette surpression étant transmise dans toute la colonne d’air jusque dans la bouche puis à l’entrée du corps de l’instrument par l’intermédiaire du bec.
Pour
travailler confortablement, on choisit d’étudier le mouvement d’une petite
quantité d’air présent initialement dans le corps de la flûte à la sortie du
bec. Cette quantité d’air occupe un petit volume qui va être soumis à une
variation de pression du côté du bec alors que la pression du côté de
l’extrémité de la flûte n’a pas varié. Comme la pression est une force (par
unité de surface), l’élément de volume de gaz va pouvoir se mettre en
mouvement. On comprend donc comment mettre en mouvement l’air dans
Après avoir mis en équation le mouvement de la petite quantité d’air initialement située au voisinage du bec sous l’effet de la force de pression et en ayant tenu compte des déformations de cette quantité d’air liées à sa compressibilité, on obtient une équation connue. L’équation de D’Alembert, identique à celle obtenue dans de nombreux phénomènes ondulatoires (ondes lumineuses, ondes électromagnétiques...). La solution de cette équation montre que le mouvement de la « tranche » d’air se transmet de proche en proche aux tranches d’air voisines avec une vitesse qui dépend des coefficients intervenant dans l’équation. Dans le cas présent, cette vitesse dépend du coefficient de compressibilité et de la masse volumique de l’air (ces deux grandeurs dépendant elles même, entre autre, de la température !). On peut à ce stade de notre étude exprimer la vitesse de propagation du son dans l’air.
Cependant
l’étude n’est pas finie, en effet, la propagation de proche en proche des
tranches d’air va finalement atteindre la tranche d’air située à l’extrémité de
la flûte et le phénomène de propagation va être perturbé par le fait que les
conditions de propagation de l’air sont modifiées. Jusqu’à présent les tranches
d’air mises en mouvement étaient confinées à l’intérieur de
On caractérise l’onde stationnaire créée par la distance séparant deux nœuds de déplacements que l’on nomme demi longueur d’onde (l/2) de l’onde formée. La longueur d’onde est reliée dans les solutions de l’équation de D’Alembert à la façon dont l’onde évolue temporellement, en particulier à la façon dont l’amplitude des ventres de déplacement et de pression évolue au cours du temps. On observe que cette amplitude évolue périodiquement, c’est-à-dire de façon régulière, l’intervalle de temps séparant deux instant où l’amplitude d’un ventre de déplacement (ou de pression) est maximale étant constant. Le phénomène ondulatoire installé dans la flûte est donc périodique, c’est-à-dire que c’est un phénomène se reproduisant identique à lui-même à intervalle de temps régulier. La période dépend de la longueur d’onde de l’onde stationnaire dans la flûte et des propriétés de l’air, en particulier de la vitesse du son. En modifiant la longueur d’onde de l’onde stationnaire formée dans la flûte il est donc possible de modifier la période (et la fréquence car la fréquence d’un phénomène est simplement l’inverse de sa période) du phénomène ondulatoire.
L’air vibrant dans la flûte de façon périodique transmet ses vibrations à l’air extérieur (nous n’avons pas étudié cette transmission dans ce mémoire) et ces vibrations périodiques sont ensuite transmises de proche en proche dans le milieu extérieur, quasiment de la même façon que l’onde progressive étudiée initialement dans le corps de la flûte, la seule différence étant que la propagation ne se fait plus uniquement dans la direction du corps de la flûte (propagation unidirectionnelle) mais dans toutes les directions (onde sphérique). Cette vibration périodique arrive alors jusqu’au tympan de l’auditeur. L’information est transmise au cerveau et ce dernier les interprète comme des notes de musiques (voir à ce sujet le paragraphe II de cette partie).
I-1. Equation des tuyaux sonores.
Un son est représenté en physique par une onde acoustique, c’est-à-dire par l’établissement d’oscillations dans un milieu continu (liquide, gaz, solide). Pour décrire ces oscillations, on considère un petit élément de volume dans le milieu et on étudie ses déplacements autour de la position qu’il occupe lorsque le milieu est au repos.
Dans le cadre de ce mémoire, le milieu de propagation de l’onde acoustique est l’air.
I-1.1. Notations utilisées.
On souhaite étudier les déplacements d’un petit élément de volume du gaz et étudier comment ces déplacements se transmettent aux éléments de volumes voisins.
On considère le corps de la flûte comme un cylindre (perce cylindrique), on travaille sur une « tranche » de gaz comprise, lorsque l’air est au repos, entre les plans d’abscisse x et (x+dx).
La notation dx représentant en physique un élément de longueur infinitésimal, c’est-à-dire aussi petit qu’on le veut pour les calculs mais non nul.
![]() x x+dx X
x x+dx X
![]()
· Déplacement x.
On note x(x,t) le déplacement par rapport à sa position de repos du plan d’abscisse x, à l’instant t.
Ainsi à l’instant t, la tranche de gaz occupe le volume compris entre les plans (x+ x(x,t)) et
(x+dx+ x(x+dx,t)).
·
Dilatation d
A priori, x(x,t) est différent de x(x+dx,t) donc le volume de la tranche de gaz peut varier au cours de la propagation, il faudra donc tenir compte des dilatations possibles du gaz. On note
d=dx/dx la dilatation de la tranche de gaz. Il s’agit en fait de la variation relative du volume de la tranche :[(volume à l’instant t - volume initial)/volume initial] lorsque l’épaisseur dx de la tranche est très petite : d=dV/V
· Compressibilité isotherme cT, relation entre dilatation et surpression.
En thermodynamique on caractérise les comportements d’un système à l’aide d’un petit nombre de variables (les variables d’états) température T, volume V, pression P. En fonction du fluide étudié, il est possible de relier dans certaines conditions, certains de ces paramètres entre eux. On obtient alors une équation qualifiée d’équation d’état permettant d’exprimer par exemple le volume comme une fonction des deux autres variables T et P. On note V=V(T,P). Mathématiquement, il est alors possible d’exprimer la façon dont varie V lorsque T et P varient, à l’aide de la différenciation de la fonction :
DV= ¶V/¶P.DP + ¶V/¶T.DT + reste infinitésimal (négligé par la suite).
Si
On peut réécrire cette formule : DV= -V0cT.DP où V0 représente le volume du fluide « au repos ». Alors cT représente la variation relative de volume par rapport à la variation de pression qui l’a provoquée pour un système évoluant à température constante.
cT=-1/V ¶V/¶P à température constante (on utilise un signe – car lorsque DP>0, c’est-à-dire lorsqu’on augmente la pression, le volume diminue pour la plupart des gaz DV<0 et il est plus agréable de manipuler des nombres positifs). cT s’appelle la compressibilité isotherme du gaz, c’est une caractéristique du gaz.
On peut donc relier la dilatation d du gaz à la variation de pression qui lui donne naissance DP à l’aide de la compressibilité isotherme par la relation :
d=DV/V=-cT DP.
· Compressibilité isentropique cS, relation entre dilatation et surpression.
Le raisonnement précédent définissant la compressibilité
isotherme et la relation entre dilatation et surpression peut se refaire en ne
considérant plus une évolution isotherme mais une évolution adiabatique
réversible. C’est-à-dire que la température n’est plus considérée comme
constante, en revanche, on considère que le gaz ne reçoit pas de chaleur au
cours de l’évolution, ce qui est acceptable si les mouvements de la tranche de
gaz sont assez rapides pour que le gaz n’ait pas le temps de recevoir beaucoup
d’énergie thermique (chaleur) au cours son évolution. On considère également
qu’à tout instant le gaz est en équilibre thermodynamique local, c’est-à-dire
qu’il est possible de définir son état à chaque instant et en chaque point en
fonction des variables d’états. Dans ce cas, la grandeur physique qui reste
constante n’est plus
Alors pour une telle transformation, on peut écrire : d=DV/V=-cS DP.
Avec cS=-1/V ¶V/¶P (à entropie constante).
cS s’appelle la compressibilité isentropique.
· Vitesse et accélération.
On peut également définir la vitesse de déplacement de la tranche de gaz en prenant v=dx/dt et son accélération en prenant a= d2x/dt2.
I-1.2. Modélisation de l’air.[2]
Pour décrire l’évolution de la tranche de gaz, il faut modéliser le gaz et exprimer sa compressibilité isentropique. On considère l’air comme un gaz parfait. C’est le modèle le plus simple pour un gaz, dans lequel on considère que les molécules d’air sont identiques, de volume très faible, sans interaction entre elles. Ce modèle est pleinement justifié pour l’air dans les conditions d’utilisation d’une flûte.
Pour un gaz parfait évoluant de façon adiabatique et réversible (c’est la modélisation la plus adaptée à l’expérience étudiée), on peut démontrer que la relation suivante est vérifiée :
P.Vg=constante=P0.V0g.
Ou g est un coefficient caractérisant le gaz étudié.
Alors
cS=-1/V. ¶V/¶P = 1/(gP)» 1/(gP0)
Pour de l’air g=1,4,
à
I-1.3. Equation du mouvement de la tranche de gaz.
Pour étudier le mouvement de la tranche de gaz, on doit appliquer le principe fondamental de la dynamique (ou 2ième loi de Newton) qui relie l’accélération d’un système matériel (en réalité de son centre de masse) a et sa masse m à la somme des forces qui s’exercent sur l’objet SF(dans un référentiel galiléen):
ma=SF
Ici l’objet dont on étudie le mouvement est la tranche de gaz de masse m=m.S.dx où m est la masse volumique de la tranche, S la section cylindrique de la flûte et dx l’épaisseur de la tranche (ainsi S.dx est le volume de la tranche de gaz).
Les forces qui s’exercent sur la tranche sont les forces de pression qui s’exercent respectivement sur le plan d’abscisse x : S.p(x,t) et sur le plan d’abscisse (x+dx) :- S.p(x+dx,t)
Remarque : Dans les forces de pression, on ne prend en compte que les surpressions, c’est-à-dire l’augmentation algébrique de la pression par rapport à la pression atmosphérique ( ce qui est justifié car on effectue une différence).
Alors la relation fondamentale de la dynamique s’écrit :
S.dx.m. ¶2x/¶t2 = -S.p(x+dx,t)+S.p(x,t)
Û dx.m. ¶2x/¶t2=-[p(x+dx,t)-p(x,t)]
Û dx.m. ¶2x/¶t2=-¶p/¶x.dx
Or p=-d/cS (voir précédemment, on a juste
changé la notation DP par p) et d=dx/dx
donc p=-1/cS. ¶x/¶x et ¶p/¶x=-1/cS. ¶2x/¶x2
La relation fondamentale de la dynamique implique donc
Û dx.m. ¶2x/¶t2=-¶p/¶x.dx
Û dx.m. ¶2x/¶t2=1/cS. ¶2x/¶x2.dx
Û cS.m.
¶2x/¶t2= ¶2x/¶x2
Cette équation est l’équation de propagation des ondes planes (c’est l’équation de D’Alembert pour une propagation dans une seule direction).
I-2. Solution de l’équation.
I-2.1. Solution générale.
L’équation obtenue précédemment est une équation connue en physique qui se retrouve dans un grand nombre de situations (ondes électromagnétiques, propagation le long d’une corde....). De façon générale, cette équation a pour forme :
1/c2. ¶2x/¶t2= ¶2x/¶x2
ou c2 représente le carré de la célérité (vitesse) de l’onde dans le milieu considéré.
Ainsi dans la flûte il y a une propagation d’ondes planes à la vitesse c =1/ÖmcS. c représente dans le cas présent la vitesse du son dans le gaz considéré.
En prenant pour l’air cS=0,7.10-5Pa-1 et m=1,3 kg.m-3 on obtient c=332m.s-1.
Mathématiquement, on montre que la solution générale de cette équation est de la forme :
x(x,t)=f(t-x/c)+g(t+x/c)
f et g étant des fonctions à priori quelconques que l’on détermine en fonction des conditions expérimentales. Ici, ces fonctions seront déterminées par la forme de la flûte, par les trous ouverts ou bouchés et par le flux d’air envoyé dans la flûte.
Le terme f(t-x/c) représente une onde se propageant dans le sens des x croissants. En effet, si à l’instant t=0 l’onde a la valeur f0 au point x0, à l’instant t, on retrouve la valeur f0 au point x vérifiant f(t-x/c)=f0=f(-x/c0) Û t-x/c=-x0/c Û x=x0+c.t >x0 donc en un point x situé après le point x0. Inversement, le terme g(t+x/c) représente une onde se propageant dans le sens des x décroissants.
En fonction de la flûte, des trous ouverts et bouchés et
de la façon « d’amorcer » l’émission par le souffle, on peut
envisager toute sorte d’onde dans
I-2.2. Système d’ondes stationnaires sinusoïdales.
Comme la flûte n’est pas de longueur infinie, il se produit une discontinuité à son extrémité qui induit un phénomène de réflexion partielle de l’onde incidente.

flûte extérieur
![]() 0 L x
0 L x
Pour aborder cette étude, considérons tout d’abord un tuyau fermé en son extrémité en x=L.
Soit xi(x,t)=f(t-x/c) le déplacement de l’onde incidente, xr(x,t)=g(t+x/c) celui de l’onde réfléchie. A l’abscisse x=L correspondant à l’extrémité fermée du tuyau, le déplacement doit être nul. On doit donc avoir xi+ xr=0 "t.
Soit f(t-L/c)+g(t+L/c) =0 "t Û g(t)
= -f(t-2L/c) (en effectuant un changement de variable
t’=t+L/c)
soit xr(x,t)=-f(t-(2L-x)/c)
Le déplacement de l’onde résultante est donc x(x,t)= xi(x,t)+ xr(x,t)=f(t-x/c)-f(t+(x-2L)/c)
Pour une raison qui sera expliqué au paragraphe II de cette partie, il est particulièrement important d’étudier les ondes sinusoïdales. Supposons donc que le musicien parvienne a exciter une onde incidente sinusoïdale d’expression xi(x,t)=A cos w(t-x/c) (A est l’amplitude de l’onde, w sa pulsation).
Alors l’onde résultante a pour expression :
x(x,t)= A cos w(t-x/c)-A cos w(t+(x-2L)/c)= - 2A sin w((L-x)/c).sin w(t-L/c)
En effet cos p-cos q=-2 sin((p+q)/2).sin((p-q)/2).
On remarque que tous les points du fluide oscillent soit en phase soit en opposition de phase, il n’y a donc plus réellement de propagation. On dit qu’il s’agit d’une onde stationnaire.
I-2.3. Nœuds et ventres de déplacement et de pression.
Pour préciser la notion d’onde
stationnaire, on peut remarquer qu’en certains points du tube, le déplacement
et toujours nul, quel que soit l’instant t considéré. Ce sont les points
vérifiants : sin w(L-x)/c = 0 Û L-x
=npc/w
avec n=1,2,...Û
x=L-nl/2 en posant l=2pc/w.
l s'appelle la longueur d'onde de l'onde stationnaire. Elle représente l’extension spatiale de l’onde considérée.
Les points vérifiant cette condition sont appelés les nœuds de déplacement.
On remarque également qu’en d’autres points, l’amplitude du déplacement est maximale. Ce sont les points vérifiants ½sin w(L-x)/c½=1Û x=L-l/4-nl/2 avec n=1,2,...
Ces points correspondent aux ventres de déplacement.
Connaissant l’expression du déplacement x(x,t), on peut en déduire l’expression de la surpression par la formule :
p=-1/cS. ¶x/¶x=2Aw/ (cS c). cos w((L-x)/c).sin w(t-L/c)
Ainsi les nœuds de pression correspondent aux ventres de déplacement et les ventres de pression correspondent aux nœuds de déplacement.
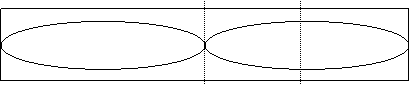
Exemple : Position des nœuds et ventres dans le cas d’une onde de longueur d’onde l=L
![]() Déplacement :
Ventre Nœud V N
Déplacement :
Ventre Nœud V N
0
![]() L
L
Pression : N V N V
Même onde à un instant différent :
![]()
![]()
![]()
![]()
![]()
![]()

On observe que l’amplitude de l’onde a varié localement mais les nœuds et les ventres n’ont pas bougé, ce qui justifie le terme d’onde stationnaire.
I-2.4. Tuyau ouvert à une extrémité.
Si le tuyau est ouvert à une extrémité, cela revient à imposer une surpression nulle à cette extrémité du tuyau (la pression à l’extérieur étant égale à la pression atmosphérique et en considérant que la pression varie de façon continue dans le gaz). Ainsi cela revient à imposer la position d’un nœud de pression en x=L et donc un ventre de déplacement en cette position.
Cela permet d’écrire l’expression de l’onde stationnaire :
x(x,t)= 2A cos w((L-x)/c).sin w(t-L/c)
Comme le tuyau est fermé à l’entrée en x=0, on doit avoir un nœud de déplacement en x=0 "t donc l’onde doit vérifier A.cos (wL/c)=0 soit w=(n+1/2) pc/L avec n=1,2,...
cette condition est équivalente à : L=(n+1/2)l/2
I-2.5. Tuyau ouvert aux deux extrémités.
On considère généralement les flûtes comme des tuyaux ouverts aux deux extrémités[3].
Dans ce cas, l’expression obtenue précédemment pour la condition en x=L reste vérifiée :
x(x,t)= 2A cos w((L-x)/c).sin w(t-L/c)
Mais comme le tuyau est ouvert à l’entrée en x=0, on doit avoir un nœud de pression en x=0 donc un ventre de déplacement. "t l’onde doit donc vérifier ½cos (wL/c) ½=1 soit w=n pc/L avec n=1,2,...
Soit l=2L/n (en effet w=2pc/l)
Ainsi toutes les longueurs d’onde ne sont pas autorisées dans le tuyau, seules les ondes stationnaires vérifiant la condition précédente peuvent apparaître dans la flûte.
La longueur d’onde la plus élevée est l0=2L, la pulsation correspondante étant w0=pc/L et la fréquence correspondante
f0=w0/2p=c/2L
Cette loi est la loi de Bernoulli[4] pour les tuyaux ouverts aux deux bouts. Cette loi permet de calculer la hauteur du son donné par un tuyau ouvert aux deux extrémités.
Remarque : Dans un tuyau ouvert, le nœud de pression n’est en fait pas exactement situé dans le plan terminal du tuyau mais un peu au-delà, à une distance proportionnelle au diamètre du tuyau. La longueur effective[5] du tuyau est donc légèrement supérieure à sa longueur géométrique.
La formule ainsi que la remarque précédente permettront de déterminer la longueur à donner à une flûte pour l’accorder. Nous y reviendrons dans le paragraphe suivant.
Notons qu’en général plusieurs ondes stationnaires se trouvent émises simultanément dans la flûte mais que toutes ces ondes doivent vérifier les contraintes précédemment établies (position de certains ventres et nœuds de pression imposée).
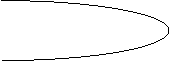
Exemple : Position des nœuds et ventres dans le cas
d’une flûte pour la longueur d’onde l0.
On représente la longueur effective de
Déplacement : Ventre
![]()
![]()
![]()
![]()
![]()
![]()
l0=2L et f0=w0/2p=c/2L
![]() 0 L
0 L
(Pression : Nœud)
Si on désire modifier la longueur d’onde de l’onde stationnaire créée, on peut imposer en certains points de l’instrument d’autres nœuds de pression, c’est ce que l’on fait en laissant ouverts certains trous.
Par exemple pour émettre une onde de longueur d’onde l1=l0/2 (correspondant à n=2), on peut imposer un second ventre de pression comme le schéma suivant le montre.
![]()
![]()
![]() trou
trou
![]()
![]()

0 L l1=l0/2 et f1=c/L
En disposant plusieurs trous sur le corps de la flûte, on parvient ainsi à imposer des systèmes d’ondes stationnaires de longueur d’onde déterminée dans la flûte, ce qui permettra d’accorder l’instrument.
En réalité, l’expérience nous indique qu’il est possible de modifier continûment la hauteur d’une note en ouvrant progressivement un trou, cette remarque prouve que le fait de considérer que la position d’un trou impose la position d’un ventre de pression n’est qu’une façon approximative d’aborder les principes d’émissions sonores avec une flûte. Certains auteurs[6] considèrent que l’ouverture du trou revient à modifier la longueur effective de la flûte.
I-3. Application et critiques.
I-3.1.Emission des sons.
On considère donc que par le bec, on met en vibration la
colonne d’air située à l’intérieur de
Les rayonnements frontal et latéral s’additionnent ensuite (on dit qu’il y a un couplage entre ces rayonnements) pour créer de façon complexe l’onde acoustique externe résultante.
Cette transmission du système d’onde stationnaire de l’intérieur de la flûte vers le milieu extérieur est complexe, nous ne l’étudierons pas dans ce mémoire.
I-3.2. Réglages d’une flûte.
Pour jouer juste, une flûte doit pouvoir émettre de façon reproductible des systèmes d’ondes stationnaires dont les fréquences correspondent à celles de la gamme utilisée.
On donne les fréquences définissants les notes dans la gamme à tempérament égal[8].
|
Note |
Fréquence du fondamental en Hz |
|
Do3 |
261,6 |
|
Ré |
293,7 |
|
Mi |
329,6 |
|
Fa |
349,2 |
|
Sol |
392,0 |
|
La3 |
440 |
|
Si |
493,9 |
|
Do4 |
523,2 |
|
Ré |
587,3 |
|
Mi |
659,3 |
|
Fa |
698,5 |
|
Sol |
784,0 |
|
La |
880 |
|
Si |
987,8 |
Nous avons vu dans un paragraphe précédent que l’onde stationnaire de plus grande longueur d’onde que peut émettre une flûte a pour longueur d’onde l0=2L soit f0=c/2L, ou L représente la longueur effective de la flûte, cette longueur étant légèrement supérieure à la longueur réelle de l’instrument. Il nous est donc possible de prévoir la note émise par une flûte lorsque tous les trous sont bouchés mais nous devons déterminer la correction à apporter à la longueur réelle de la flûte pour connaître sa longueur effective.
On choisi donc une flûte soprano Yamaha en plastique dont on sait qu’elle doit émettre un do donc de fréquence multiple de f=261,6Hz lorsque tous les trous sont bouchés. On considère que la vitesse du son dans l’air est[9] 332m.s-1. Alors la longueur effective théorique est Leff=c/2f0. Si on prend f0=523,2 Hz (do4) on obtient une longueur effective de 31,7cm ce qui est proche de la longueur réelle de la flûte (mais cela revient à dire que la note la plus basse jouée par la flûte soprano est un do4 alors qu’il s’agit en réalité d’un do5, ceci s’explique peut-être par le fait que le fondamental n’est pas excité mais que c’est le premier harmonique qui domine).
La longueur mesurée (du bloc à l’extrémité) est Lmes=28cm. On va donc supposer que connaissant la longueur réelle de la flûte, on peut en déduire sa longueur effective par la formule : Leff = 31,7/28 .Lmes = 1,13.Lmes (Cette formule correctrice n’est qu’une approximation qui suppose qu’il y a une relation de proportionnalité entre Leff et Lmes).
On peut maintenant tester ces prédictions sur d’autres flûtes :
|
|
Lmes |
Leff |
f0=c/2.Leff |
Note calculée |
note jouée |
|
TénorYamaha |
58cm |
65cm |
256Hz |
do3 |
do4 |
|
Alto Yamaha |
41cm |
46cm |
358Hz |
fa3 |
fa4 |
|
Sopranino Aulos |
21cm |
24cm |
692Hz |
fa4 |
fa5 |
On remarque évidemment de petits écarts entre les
fréquences calculées et les fréquences des notes correspondantes mais pour
indiquer la note attendue, on a systématiquement choisi la note dont la
fréquence est la plus proche de celle calculée. On observe que la théorie
permet donc bien de prédire la note jouée en mesurant la longueur de
I-3.3. Critique du modèle.
Le modèle proposé donne des
résultats assez satisfaisants, il permet en particulier de prévoir
approximativement la hauteur des sons produits en fonction des trous ouverts ou
bouchés sur
La principale approximation a été de ne pas tenir compte de la façon dont les ondes sont engendrées dans la flûte par l’intermédiaire du bec. Ce bec est indispensable pour fournir l’énergie initiale et mettre l’air présent dans le corps de la flûte en mouvement. En réalité, par l’intermédiaire de ce bec on envoie de l’air avec une certaine vitesse au point x=0 du tuyau sonore. Du fait de cette vitesse, il apparaît deux problèmes venant perturber le système d’ondes stationnaires dans la flûte.
Tout d’abord, dans tout fluide en mouvement il y a modification du champ de pression à cause de la vitesse : c’est l’effet Venturi. A cause de cet effet, l’hypothèse consistant à placer un ventre de pression en x=0 et un nœud en x=L n’est pas exactement vérifiée, on peut donc penser que la pression n’a pas exactement le comportement décrit. C’est cette hypothèse qui permet certainement d’expliquer que la longueur effective du tuyau est légèrement supérieure à sa longueur réelle.
Par ailleurs, toujours à cause de la vitesse du fluide au niveau du biseau, l’air ne s’écoule pas de façon régulière (écoulement laminaire) mais peut se trouver perturbé (écoulement turbulent). A cause des tourbillons engendrés dans l’écoulement turbulent, le système d’ondes stationnaires peut être modifié.
A titre d’illustration, on donne une photographie[10] d’un jet d’air au niveau du biseau d’un tuyau d’orgue sur lequel il apparaît bien que le jet est complexe, ce qui montre que le problème est plus compliqué que notre modèle le laisse prévoir.

Ecoulement dans
un tuyau d’orgue
Cependant, il est acquis que ce sont les ondes stationnaires qui caractérisent le son émis par l’instrument, en effet, contrairement aux autres ondes qui peuvent se propager dans la flûte, elles présentent un caractère suffisamment régulier pour être identifiées comme des notes, les autres ondes n’étant qualifiées que de bruit.
Pour une description plus précise des mécanismes d’émission par la flûte il faudrait également tenir compte de la forme de la perce qui n’est pas cylindrique pour toutes les flûtes, de la forme des trous, du bec, de la nature du matériau, de la façon de souffler dans la flûte...
Compte tenu de la complexité du problème soulevé, il est préférable de tenter de poursuivre l’étude de l’instrument expérimentalement. Dans la seconde partie de ce mémoire, on étudiera donc quelques caractéristiques des ondes de manière expérimentale. Auparavant il faut justifier l’importance des ondes sinusoïdales utilisées précédemment, définir précisément la justesse d’un instrument, son timbre et avant tout indiquer ce qu’est une note de musique.
II-Analyse
harmonique.
II-1.
Bruits et sons.
Dans le chapitre précédent, on a étudié les processus d’émission des sons dans une flûte sans se préoccuper de musique. On doit maintenant définir un son musical. En musique, on considère qu’un son musical est caractérisé par une onde acoustique périodique alors que l’onde associée à un bruit n’est pas périodique. Rappelons qu’un signal est périodique s’il se reproduit identique à lui même à intervalle de temps régulier. Pour caractériser un signal périodique, on définit sa période T comme étant l’intervalle temporel séparant deux reproductions du signal à l’identique. On peut également définir la fréquence f du signal comme le nombre de reproduction du signal par seconde, naturellement T=1/f . On peut également relier la période à la pulsation w du signal par la relation : T=2p/w. Une onde stationnaire correspond à un signal périodique, donc à un son musical. Il faut maintenant justifier l’utilisation des ondes sinusoïdales.
II-2. Spectre d’un son.
Tout signal périodique sera donc interprété comme un son par le cerveau humain, il est donc important de décrire précisément ce type de signal. Pour cela on utilise la théorie établie par Fourier concernant les signaux périodiques.
II-2.1.
Décomposition en série de Fourier.[11]
Considérons un signal s(t) périodique de période T=2p/w. A tout instant où le signal est continu (c’est le cas des ondes acoustiques étudiées), il peut se développer comme une série de fonctions sinusoïdales de la façon suivante :
s(t)=A0/2 + å[Ak cos(kwt)+Bk sin(kwt)]
avec Ak=2/T.ò s(t) cos(kwt)dt et Bk=2/T. ò s(t).sin(kwt) dt
Remarque : Pour une fonction paire Bk=0, pour une fonction impaire Ak=0.
Ainsi, tout signal périodique peut s’écrire comme l’addition de signaux sinusoïdaux, d’où l’importance qu’il y a à étudier les ondes sinusoïdales, en effet, quel que soit le signal périodique étudié, il sera toujours possible pour l’analyser d’étudier l’évolution des différentes sinusoïdes qui le composent.
II-2.2. Spectre du signal.
On peut réécrire :
s(t)= S0+åsk
S0 est la composante continue du signal, sk(t)=Ak.cos(kwt) + Bk.sin(kwt)
s1(t)=
A1.cos(wt)+B1.sin(wt)
sk(t)=Ak.cos(kwt)+Bk.sin(kwt)=Ck.cos(kwt+fk) avec Ck=ÖAk2+Bk2
et tan fk=-Bk/Ak
Alors s1 s’appelle l’harmonique de rang 1 ou fondamental du signal étudié, sk est l’harmonique de rang k. L’ensemble des Ck représente le spectre de fréquence de s(t), on peut le représenter sur un graphe donnant Ck en fonction de w, l, f...
Pour reconstituer le signal s(t) à partir de son spectre, il suffit d’effectuer la somme des différents harmoniques.
II-2.3. Exemples de décomposition en série de
Fourier.
A titre d’exemple cherchons à déterminer le spectre de 2 fonctions périodiques simples :
· Fonction sinusoïdale s(t)= A sin (wt)
C’est une fonction impaire, donc Ak=0 "k.
Bk=2A/T. ò sin(wt).sin(kwt).dt = A/T. ò cos[(1-k)wt]dt - A/T. ò cos[(1+k)wt]dt
car 2
sina sinb = cos(a-b) -cos(a+b)
si k=1 B1=A si k¹1 Bk=0
Le spectre se compose donc uniquement du fondamental de pulsation w.
![]() Ck
Ck
![]()
![]() A
A
![]() w
w
w 2w 3w
· Fonction “créneau”
On désire déterminer le spectre de la fonction s(t) représentée ci-dessous:
![]() s(t)
s(t)
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]() t
t
0 T
C’est une fonction impaire, donc Ak=0 "k.
Bk=2/T. ò s(t).sin(kwt)dt = 2A/T{ -ò sin(kwt).dt + ò sin(kwt).dt}
Û Bk = 2A/T.{+[cos(kwt)/kw] - [cos(kwt)/kw] }
Û Bk = -2A/kp.[1-cos(kp)]
(rappel:w=2p/T donc w.T/2=p)
si k est pair alors cos(kp)=1 donc Bk=0
si k est impair alors cos(kp)=-1 donc Bk=-4A/kp.
La décomposition en séries de Fourier de ce signal créneau ne contient donc que les harmoniques impaires, le coefficient Ck étant inversement proportionnel à k.
![]() Ck
Ck
![]()
![]() Bo
Bo
L’échelle pour les Ck n’est pas régulière
![]()
![]() Bo/3
Bo/3
![]()
![]() Bo/5
Bo/5
Bo/7
![]()
![]()
![]() w
w
0 w 2w 3w 4w 5w 6w 7w
Pour décrire un signal périodique, on pourra représenter son spectre. Ainsi, tout son musical émis par une flûte étant un signal périodique, il peut être défini par son spectre (fondamental et harmoniques). Ce son étant produit dans la flûte par une superposition d’ondes stationnaires sinusoïdales.
En pratique, des appareils nommés analyseurs de spectre permettent d’effectuer la décomposition en séries de Fourier d’un signal périodique. Dans la partie expérimentale de ce mémoire, nous tenterons de décrire les sons émis par différentes flûtes dans différentes conditions à l’aide de tels spectres obtenus par enregistrement de son puis analyse à l’aide d’un logiciel comportant un analyseur de spectre sommaire.
II-3. Hauteur d’une note.
Un son musical est donc caractérisé par le fait qu’il est périodique. On distingue alors les différents sons musicaux par leur période, c’est-à-dire par la période du fondamental de leur spectre, ou de façon identique par la fréquence ou la pulsation du fondamental. Deux sons ayant des fondamentaux de même fréquence seront donc interprétés par le cerveau comme des notes de même hauteur.
On peut donc définir chaque note par la fréquence du fondamental. Cette définition a évolué au cours du temps, actuellement les orchestres symphoniques prennent souvent pour définition du la3 la fréquence 440Hz, voire 442Hz, mais on rencontre de nombreux instruments pour lesquels la définition de ce la est différente, par exemple 415Hz pour certains instruments baroques.
II-4. Timbre d’un instrument.
Choisir la hauteur d’une note, c’est choisir la période de l’onde associée, ce qui revient à choisir la fréquence du fondamental du spectre. Avec une flûte cette sélection se fait en imposant la position de différents nœuds et ventres de pression dans le corps de l’instrument. Lorsqu’une onde peut s’installer dans la flûte, il est possible que d’autres ondes respectant également les contraintes se superposent à la première, voir par exemple dans le paragraphe I-2.4., sur le schéma de l’onde l0, on peut ajouter l’onde l1 qui respecte les contraintes imposées, en revanche sur l’onde l1, on ne peut pas ajouter l’onde l0 qui ne respecte pas la position du ventre imposé par le trou ouvert. La plupart du temps c’est ce qui se produit et l’onde émise ne se limite pas à une onde stationnaire sinusoïdale. Le spectre émis compte un grand nombre d’harmoniques. En général le son produit est identifié comme une seule note dont la hauteur est déterminée par la fréquence du fondamental, mais dans certaines situations, les rapports des fréquences entres les différents harmoniques sont tels que l’on identifie plusieurs notes, on parle alors de sons multiphoniques.
Si lors de l’émission d’une note, on ne produisait que le fondamental, c’est-à-dire une sinusoïde parfaite, il ne serait pas possible de distinguer les instruments entre eux, c’est donc le spectre émis qui permet de reconnaître tel ou tel instrument. Le spectre émis caractérise donc le timbre de l’instrument.
Pour étudier un instrument de manière à identifier « scientifiquement » ses caractéristiques afin de pouvoir en tirer des sons de la meilleure qualité possible ou pour améliorer la facture, il est donc intéressant d’étudier le spectre de l’instrument. Actuellement, un grand nombre de recherches en acoustique musicale repose sur des analyses spectrales. C’est aussi l’objet de la partie expérimentale de ce mémoire. A l’aide d’observations sur les spectres émis dans différentes conditions, on va tenter d’énoncer quelques caractéristiques de l’émission sonore à l’aide d’une flûte. Il faut auparavant noter que l’étude des instruments par analyse spectrale est encore très loin d’offrir des résultats aussi convaincants que ceux obtenus par la pratique des interprètes lorsqu’il s’agit de tirer le plus grand profit d’un instrument existant ou par les facteurs lorsqu’il s’agit de créer ou de régler un instrument. Il n’est pas possible de restreindre la musique à une analyse harmonique, le spectre émis étant en général plus complexe que ceux décrits précédemment. Cela apparaît d’ailleurs dans le fait qu’il n’existe encore pas de synthétiseur capable de reproduire fidèlement le timbre, les attaques, la sonorité des flûtes à bec ou d’autres instruments, alors qu’il est facile d’émettre des signaux quasi-sinusoïdaux à l’aide de dispositifs électro-acoustique simples. Cela prouve qu’il n’est pas possible de restreindre les caractéristiques d’un instrument à son spectre obtenu par décomposition en séries de Fourier. Le paragraphe qui suit tente d’aborder les causes de ces restrictions.
II-5. Attaques, turbulence...
La décomposition en séries de Fourier n’est valable que pour un signal périodique, c’est-à-dire un signal qui se répète identique à lui-même à intervalle de temps régulier. Mais si le son étudié est émis à un instant donné pour s’arrêter un instant plus tard, ce signal n’est pas périodique mathématiquement car il cesse de se reproduire identiquement à lui-même. La décomposition en série de Fourier n’est donc possible théoriquement que sur des sons qui durent depuis un temps infini et ne cessent jamais. Comme le son commence à un moment donné, le spectre obtenu par décomposition en série n’est juste que de façon approximative. On considère d’ailleurs en acoustique qu’un instrument s’identifie en grande partie par ses attaques, c’est-à-dire précisément par ce qui fait que l’analyse spectrale n’est pas justifiée. Pour améliorer le modèle on peut utiliser l’opération de transformée de Fourier adaptée aux signaux non périodiques. Cette transformation repose sur le même principe d’analyse spectrale que la décomposition en série mais, alors que la décomposition en série donne un spectre discret, c’est-à-dire quelques harmoniques bien séparés, la transformée de Fourier donne un spectre continu, dans lequel on trouve des composantes harmoniques à toutes les fréquences et pas seulement aux fréquences multiples du fondamental.
En plus de l’attaque qui oblige à déterminer la transformée de Fourier du signal, les problèmes de turbulence évoqués au paragraphe I-3. et les ondes autres que stationnaires qui peuvent apparaître dans l’instrument ajoutent des émissions d’ondes acoustiques non périodiques qui viennent également perturber le spectre discret attendu. Ainsi le spectre d’un instrument s’obtient plutôt par transformation de Fourier du signal émis, ce spectre continu faisant cependant ressortir pour la plupart des instruments mélodiques un spectre discret comparable aux spectres obtenus par décomposition, plongé dans un bruit de fond continu plus ou moins important.
A l’aide des outils que nous avons définis dans toute cette partie théorique, il nous est désormais possible d’étudier expérimentalement quelques caractéristiques des flûtes à becs.